Matrix diagonalization is a fundamental linear algebra operation with a wide range of applications in scientific and other fields of computing. At the same time, it is also one of the most expensive operations with a formal computational complexity of $\mathcal{O}(N^3)$, which can become a significant performance bottleneck as the size of the system grows. In this post, I will introduce the canonical algorithm for diagonalizing matrices in parallel computing to set the scene for today’s main topic: improving diagonalization performance. With the help of benchmark calculations, I will then demonstrate how a clever mathematical library choice can easily reduce the time needed to diagonalize a matrix by at least 50 %.

It has been a hectic late winter–early spring for me as I have been gathering data for the last manuscript to be included in my Ph.D. thesis. Unfortunately, as a result, I haven’t had the time to write any new posts in quite a while, although I had a number of topics already pre-planned. After a feverish couple weeks of writing, I can finally see the finish line in sight and I expect to have the manuscript submission ready in a few days. This has finally given me the opportunity to write up today’s post.

As mentioned above, this post will focus on matrix diagonalization in parallel computing. I will introduce a nifty library for drastically boosting diagonalization performance without requiring extensive code modifications. The algorithms involved are briefly discussed to give you an understanding of the origins of the speed improvement. This post concludes my three-part miniseries on parallel programming using the message passing interface (MPI) paradigm, at least for the foreseeable future. You can find my previous posts related to MPI I/O here and here.

PS. You might notice that some of the symbols and equations in this post have been typeset in $\LaTeX$-esque fashion (to see the proper font rendering, you need to enable JavaScript ). I followed the instructions here to enable MathJax in Hugo for displaying mathematical expressions. Note to other Hugo users interested in MathJax support, you might have to escape some characters you normally wouldn’t to get an equation to render properly, e.g., subscripts need to be written as B\_{11}, not B_{11}.

Table of Contents

Representing matrices in parallel computing

Before discussing how matrices are diagonalized, I will first take a small detour and describe how matrices are represented in MPI based parallel applications. If you are already familiar with the concepts, feel free to skip ahead to the next section.

Matrices with a large degree of nonzero elements, so-called full or dense matrices, are usually represented in block cyclic format in MPI applications. This format describes how to distribute a matrix over a set of $N$ processors. Note that other storage formats are often preferable for sparse matrices, where the majority of matrix elements are zero, but I won’t cover sparse matrices or special algorithms for diagonalizing such matrices in this post.

Let’s take a closer look at the block cyclic format with the help of the following picture, which compares different cyclic and blocked distributions for one dimensional vectors and two dimensional matrices. The figure was taken from the excellent “Introduction to Parallel Computing” tutorial by Blaise Barney at the Lawrence Livermore National Laboratory.

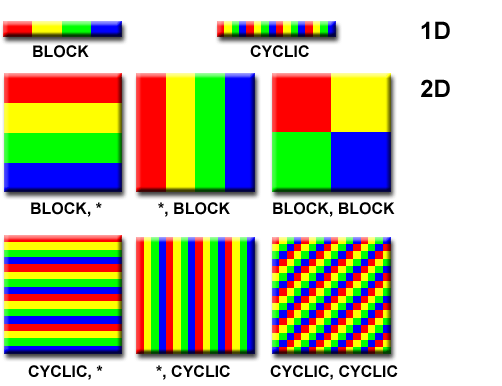Figure 1. Comparison of cyclic and block formats for representing vectors and matrices in parallel over multiple processors. Each unique color represents a different processor. The colored segments indicate the portion of the full matrix that resides in the local memory of a processor. Picture source: “Introduction to Parallel Computing” tutorial by Blaise Barney at the Lawrence Livermore National Laboratory.

In the cyclic decomposition of a matrix, each row, column or even every element of a matrix is distributed onto different processors, wrapping over the set of processors repeatedly until all elements of the matrix are exhausted. By contrast, in the block representation, the matrix is decomposed into $N$, not necessarily evenly sized, submatrices by diving the matrix along the rows, columns, or combinations of the two (“blocks”). Each submatrix is then assigned to a different processor.

What are the advantages and disadvantages of these two distributions? Keep in mind that the original design philosophy behind MPI was to create a standardized parallel computing architecture for distributed memory platforms. Consequently, each processor has its own private chunk of memory and if a processor needs to access a portion of the matrix that is not in the local memory, it must request the data from its owner via communication. The newer MPI-3 standard does allow direct shared memory programming (see e.g. here), but it might not be available on all platforms.

Taking these notions into account, we see that the cyclic distribution is superior for evenly distributing a matrix, but poor for matrix manipulations because a lot of communication is required to access adjacent matrix elements that might reside on different processors. The opposite holds true for block decomposition: linear algebra can be executed efficiently on submatrix blocks that are contiguous in memory, but there might be load balancing issues e.g. if the matrix contains “sparse” regions. The block cyclic matrix distribution attempts to combine the best qualities of both representations by decomposing the matrix into smaller blocks that are cyclically distributed among processors.

The most efficient block cyclic layout is a two dimensional layout where the total $N$ processors are arranged into a rectangular grid $N = N_{\mathrm{row}} \times N_{\mathrm{col}}$ with $N_{\mathrm{row}}$ rows and $N_{\mathrm{col}}$ columns. This distribution has been visualized below in Figure 2. The total number of matrix blocks is controlled by the size of each block, that is, the number of rows and columns included within each block. These quantities are user controllable and they often are set to the same value making the blocks square. The block sizes are adjusted accordingly in case the matrix is not evenly divisible by the total number of processors.

Figure 2. Illustration of the two dimensional block cyclic layout. In this example, a matrix with $7 \times 10$ elements (the numbered entries), or more generally collections of elements, is distributed over a $2 \times 3$ processor grid. The colors indicate how elements in the global matrix are mapped onto different processors. The distribution on the right displays the processors’ local view of the matrix.

The two dimensional block cyclic layout has been adopted in the general purpose dense matrix linear algebra package ScaLAPACK. This package is a reference library, i.e., it has been tested extensively on different platforms but the numerical performance has not been optimized for a specific architecture. Computing vendors provide their own tuned versions of the library that target specific hardware, e.g. Intel MKL or Cray Libsci, which should always be used for production calculations if available due to the significant speed advantages they offer.

Parallel matrix diagonalization with ScaLAPACK and ELPA

To recap, assume we are given a dense matrix $\boldsymbol{\mathrm{A}}$ that is distributed in parallel using MPI over a set of $N$ processors in block cyclic distribution (see above if these concepts are unclear). Our task is to diagonalize $\boldsymbol{\mathrm{A}}$ and we would like to do it as efficiently as possible.

Matrix diagonalization is intimately linked with eigenvalue problems and the eigendecomposition of a matrix. Concretely, we can define matrix diagonalization as finding the solution to the following eigenvalue problem

$$ \boldsymbol{\mathrm{A}}\boldsymbol{\mathrm{X}}=\boldsymbol{\mathrm{X}}\boldsymbol{\mathrm{\Lambda}} $$

where $\boldsymbol{\mathrm{X}}$ is a matrix that contains the eigenvectors of $\boldsymbol{\mathrm{A}}$ and $\boldsymbol{\mathrm{\Lambda}}$ is the eigenvalue matrix. The eigenvalue matrix contains the eigenvalues of $\boldsymbol{\mathrm{A}}$ on its diagonal and zeroes everywhere else. It, therefore, is the actual diagonal matrix we seek. As I shall subsequently show, computing the eigenvalue matrix requires less work than the eigenvector matrix. However, eigenvectors are often useful in their own right and it is very common that both must be computed.

Depending on the properties of $\boldsymbol{\mathrm{A}}$, there are a variety of eigenvalue algorithms we could adopt to diagonalize the matrix. For the remainder of the post, I will assume that the matrix $\boldsymbol{\mathrm{A}}$ is a symmetric real matrix (or, analogously, complex Hermitian): $\boldsymbol{\mathrm{A}} = \boldsymbol{\mathrm{A}}^\mathrm{T}$. Such matrices frequently appear in applications especially in the fields of computational chemistry and physics.

Dense matrix linear algebra packages that are based on ScaLAPACK offer three different algorithms for diagonalizing real symmetric matrices, namely, the p?syevd, p?syevx and p?syevr methods where ? accepts different values depending on the matrix data type, e.g., d for double precision matrices. These algorithms not only differ in the approach taken to diagonalize the matrix but also whether they are suitable for calculating only selected eigenvalues of the input matrix or whether all eigenvalues must always be computed.

Let’s examine the p?syevd algorithm in more detail by going through the main steps of the algorithm. For illustrative purposes, let $\boldsymbol{\mathrm{A}}$ be the following $6 \times 6 $ matrix $$ \boldsymbol{\mathrm{A}} = \begin{bmatrix} A_{11} & A_{12} & A_{13} & A_{14} & A_{15} & A_{16} \\
A_{21} & A_{22} & A_{23} & A_{24} & A_{25} & A_{26} \\
A_{31} & A_{32} & A_{33} & A_{34} & A_{35} & A_{36} \\
A_{41} & A_{42} & A_{43} & A_{44} & A_{45} & A_{46} \\
A_{51} & A_{52} & A_{53} & A_{54} & A_{55} & A_{56} \\
A_{61} & A_{62} & A_{63} & A_{64} & A_{65} & A_{66} \end{bmatrix} $$

The ScaLAPACK eigenvalue algorithm p?syevd is comprised of the following steps:

1. Reduction to tridiagonal form $\boldsymbol{\mathrm{T}}$ with Householder transformations $\boldsymbol{\mathrm{Q}}$ $$ \boldsymbol{\mathrm{T}} = \boldsymbol{\mathrm{Q}}\boldsymbol{\mathrm{A}}\boldsymbol{\mathrm{Q}} = \begin{bmatrix} A_{11} & A_{12} & 0 & \cdots & \cdots & 0 \\
   A_{21} & A_{22} & A_{23} & \ddots & \ddots & \vdots \\
   0 & A_{32} & A_{33} & A_{34} & \ddots & \vdots \\
   \vdots & \ddots & A_{43} & A_{44} & A_{45} & 0 \\
   \vdots & \ddots & \ddots & A_{54} & A_{55} & A_{56} \\
   0 & \cdots & \cdots & 0 & A_{65} & A_{66} \end{bmatrix} $$
2. Solution of tridiagonal eigenvalue problem with divide-and-conquer (DQ) algorithm $$ \boldsymbol{\mathrm{T}}\tilde{\boldsymbol{\mathrm{X}}} = \tilde{\boldsymbol{\mathrm{X}}}\boldsymbol{\mathrm{\Lambda}} $$
3. Backtransformation of eigenvectors $$ \boldsymbol{\mathrm{X}} = \boldsymbol{\mathrm{Q}}^\mathrm{T}\tilde{\boldsymbol{\mathrm{X}}} $$

The p?syevx and p?syevr methods differ from p?syevd in the second step of the algorithm: the former relies on bisection and inverse iteration, whereas the latter on the multiple relatively robust representations (MRRR) method. You can find more in-depth details about these two algorithms e.g. in this paper. Significant performance differences between these algorithms become apparent only when a subset of the eigenvalues are required, because p?syevd always returns the full set of eigenvalues, whereas the others are capable of computing individual eigenvalues. However, it is worth stressing that all eigenvalues are now necessary since our ultimate goal is to diagonalize the input matrix. In the remainder of this post, I will therefore exclusively discuss the DQ method based p?syevd algorithm.

An alternative approach to improve the performance of the DQ ScaLAPACK algorithm would be to modify steps 1 and 3 of the algorithm, that is, the reduction to tridiagonal form and the backtransformation operation. This strategy has been adopted in the Eigenvalues SoLvers for Petaflop-Applications (ELPA) library. Specifically, the direct transformation to tridiagonal form is replaced by a two-step process, where the matrix is first converted to banded form (i.e. to a matrix with more than 1 sub- and superdiagonal), and the banded matrix is subsequently reduced to tridiagonal form. The backtransformation to a full matrix is modified in analogous fashion. These choices increase the fraction of matrix-matrix linear algebra operations performed during the transformation steps and minimize the fraction of matrix-vector operations, which should lead to overall better numerical performance in the diagonalization algorithm. An optional blocked QR decomposition can be performed for further speed improvements. A detailed description of the ELPA library is given in this review article.

ELPA offers a generic Fortran kernel that should work across different architectures, as well as a host of tuned kernels for modern CPUs that support e.g. AVX, AVX2, or AVX-512 instruction sets. Even a GPU kernel has recently been implemented. ELPA is compiled with the standard configure & make approach. The interface to the ELPA diagonalization routine is very similar to the equivalent ScaLAPACK routine, which makes it a relatively straightforward task to include ELPA as an optional dependency in applications that already leverage ScaLAPACK for dense matrix diagonalization and other linear algebra operations.

Benchmarking ELPA against ScaLAPACK

Matrix diagonalization performance, in general, depends on a variety of factors:

• Size of matrix (application dependent)
• Structure of matrix (application dependent)
• Number of processors used for diagonalization (user tunable setting)
• MPI block size for matrix (user tunable setting)
• Diagonalization algorithm (user tunable setting if implementation allows it)

The first two factors are fixed for a given problem, while the latter three can be optimized at least to a degree by the user. In this section, I will compare the diagonalization performance of the ScaLAPACK p?syevd (as implemented in the Cray Libsci library) and ELPA algorithms. I will examine two square matrix sizes with $5888^2$ and $13034^2$ elements, respectively, and measure how the algorithms scale as the number of processors, $N$, is increased. The two methods will also be contrasted. The benchmark calculations are performed with the CP2K quantum chemistry software. Each data point corresponds to the average diagonalization time obtained by diagonalizing the input matrix 10 times. The simulations were repeated twice to collect better timing statistics. The CP2K input files used in this post are based on standard benchmark input files distributed with the software. You can find them in full from this link.

Disclaimer: I am in no way affiliated with ELPA. I discovered the library when I was attempting to maximize the performance of my quantum chemistry simulations. An interface to ELPA was already implemented in CP2K and I merely extended it with new features.

The benchmarks were run on a Cray XC40 supercomputer (“Sisu”) where each computational node is comprised of two 12-core Intel Xeon E5-2690v3 processors with 64 GB DDR4 memory. The matrix block size is set to 64 in both row and column dimensions. The effect of using the optional QR decomposition step in the ELPA algorithm was also gauged. Note that the QR decomposition works only with even sized matrices whose block size is $\ge 64$. The 2017.05 version of ELPA and the AVX2_BLOCK2 kernel are used throughout.

As a side note, CP2K by default limits the number of MPI processes used for diagonalization, because earlier benchmarks on a Cray XE6 machine have shown ScaLAPACK diagonalization performance to suffer when the matrix is parallelized onto too many processors relative to the size of the matrix. The ‘optimal’ number of processes for diagonalization, $M$, is computed using the heuristic

$$M = (K+a\times x-1)/(a\times x)\times a$$

where $K$ is the size of the input matrix, and $a$ and $x$ are integers with default values $a=4$ and $x=60$. If $M \lt N$, the matrix is redistributed onto $M$ processors before diagonalizing it. With ELPA, redistribution of the input matrix is performed only in the event that the calculation would otherwise crash within the ELPA library due to overparallelization, which causes some processors to hold an empty matrix block. In addition to the tests discussed above, I have also estimated the effects of the optimal number of CPUs heuristic with ScaLAPACK by either disabling the check or by using the default values.

The main benchmark results have been summarized in the figure below.

Figure 3. Diagonalization performance with ScaLAPACK (SL) and ELPA as a function of the number of MPI nodes (multiples of 24 CPU cores). At left, results are shown for the larger matrix with $13034^2$ elements; at right, for the smaller matrix with $5888^2$ elements.

These benchmarks demonstrate that ELPA is clearly faster than ScaLAPACK for diagonalizing a matrix in parallel. Depending on the number of processors used, ELPA outperforms ScaLAPACK by 60-80 % in the case of the larger matrix and by 50-70 % in the case of the smaller matrix. Using the optional QR decomposition feature of ELPA results in a further improvement, which interestingly becomes larger and larger as the number of processors grows. The diagonalization scalability saturates at 12 nodes for the larger system and at 4 nodes for the smaller system.

I also tested the effectiveness of limiting the total number of MPI processors for diagonalization with ScaLAPACK. The results are shown in the figure below. At least for the tested systems, the redistribution strategy seems to be ineffective and using all available cores is the preferable choice even with ScaLAPACK. More extensive testing on different platforms and other systems is however required before deciding whether the redistribution step can safely be removed from CP2K.

Figure 4. Total simulation runtime as a function of the number of MPI nodes (multiples of 24 CPU cores) with ScaLAPACK. The data marked in red was obtained by limiting the total number of processors used for diagonalization using the heuristic discussed above. At left, results are shown for the larger matrix with $13034^2$ elements (220 core limit); at right, for the smaller matrix with $5888^2$ elements (100 core limit).

Conclusions

In this post, I discussed algorithms for diagonalizing dense matrices in the context of MPI parallelized, distributed memory applications. I showed that the algorithm implemented in the ELPA library clearly outperforms the ScaLAPACK equivalent by at least 50 %. Because the diagonalization routine interface in ELPA is very similar to ScaLAPACK, introducing ELPA as an optional replacement for ScaLAPACK in diagonalization intensive MPI applications should be relatively straightforward to implement and could lead to significant savings in computational time.